
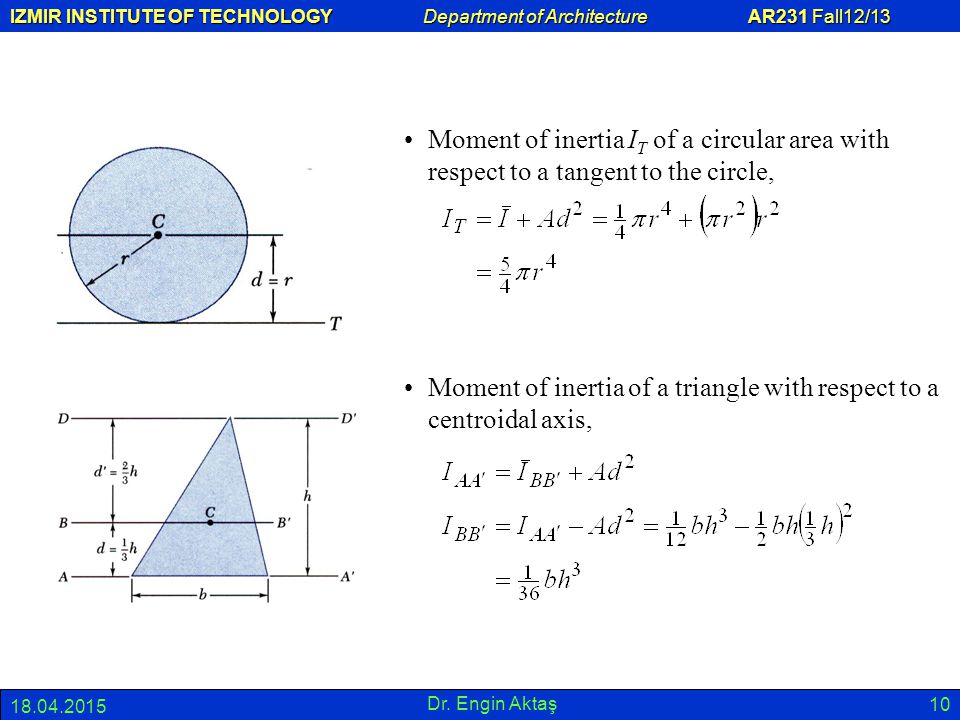

This is important, since the moment of inertia will vary depending on the axis chosen.
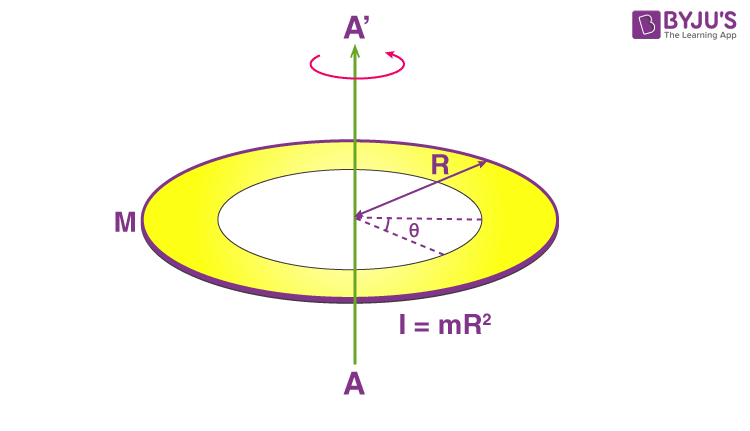
To determine the area moment of inertia, start by drawing out the area under analysis, and include the axes you are taking the moment of inertia about. The x and y terms inside the integral denote the centroidal position of the differential area measured from the y and x axes. We can deconstruct the sheet or slab into rods, each of which rotates about the axis of rotation of the sheet.Ĭalculate the moment of inertia of a uniform rigid rod of length $l$ and mass $m$ about an axis perpendicular to the rod (the $y$-axis) and passing through its center of mass. Calculating the Rectangular Area Moment of Inertia via Integration. Moment of inertia about the x-axis: displaystyle Ix int y2, dA. This may or not be what you're after, but here is one method we could use to derive the result rather than simply look it up. If we add all to masses together and take the limit as the rectangle size goes to zero, we get a double integral. As mentioned earlier, the moment of inertia of a particle of mass about an axis is where is the distance of the particle from the axis, also known as the radius of gyration. Re: I no longer own a Calculus book what formula is this that I need


 0 kommentar(er)
0 kommentar(er)
